Metropolis
Basic Principle
- Metropolis is an iterative model
- At each iteration, four models are run successively (network skims computation, pre-day model, within-day model and day-to-day model)
- The simulation stops when a convergence criteria is met or when the maximum number of iterations is reached
Network skims computation
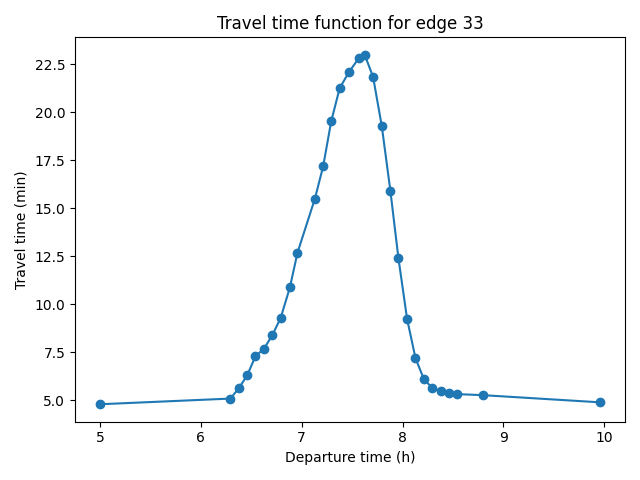
- Input: time-dependent travel-time function for each road of the road-network graph
- Step 1: compute a time-dependent Hierarchy Overlay of the graph
- Step 2: compute search spaces for each origin and destination node
- Step 3: compute profile queries for each origin-destination pair
- Output: time-dependent travel-time function for each origin-destination pair (with at least one trip)
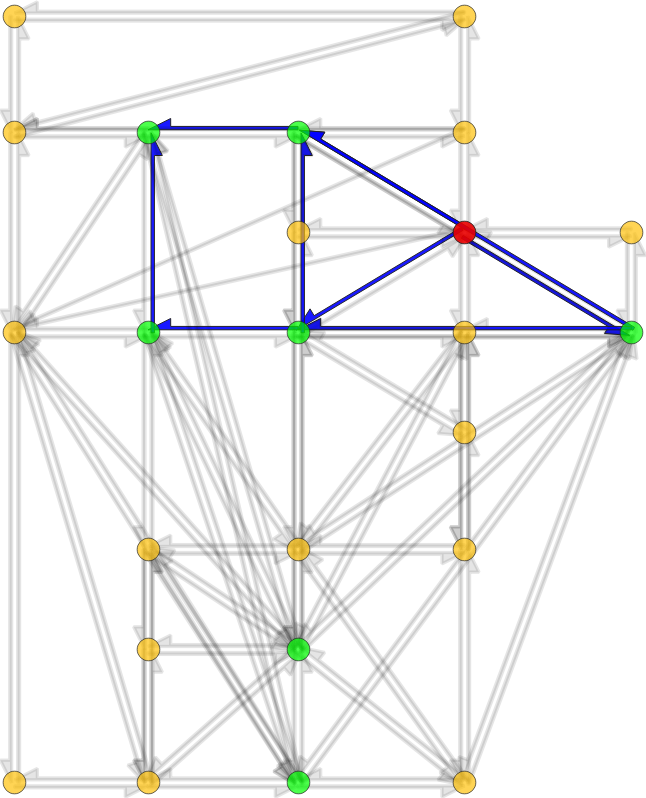
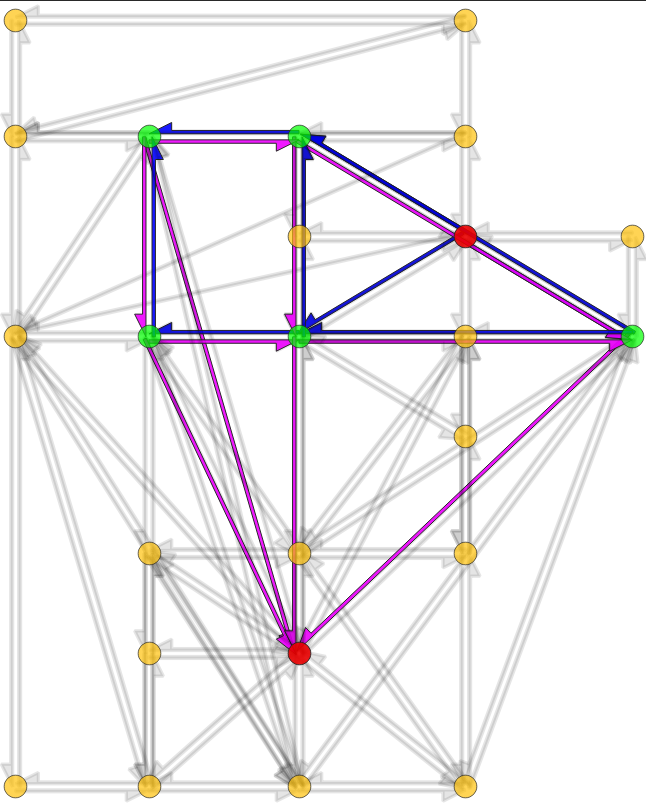
Geisberger, R. and Sanders, P., 2010. Engineering time-dependent many-to-many shortest paths computation. In 10th Workshop on Algorithmic Approaches for Transportation Modelling, Optimization, and Systems (ATMOS'10). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik.
Pre-Day Model
- Input: time-dependent travel-time function for each origin-destination pair
- Departure-time choice: choose the departure time of the agent, given the travel-time function, the schedule-utility and travel-utility functions and the mode (continuous Logit model)
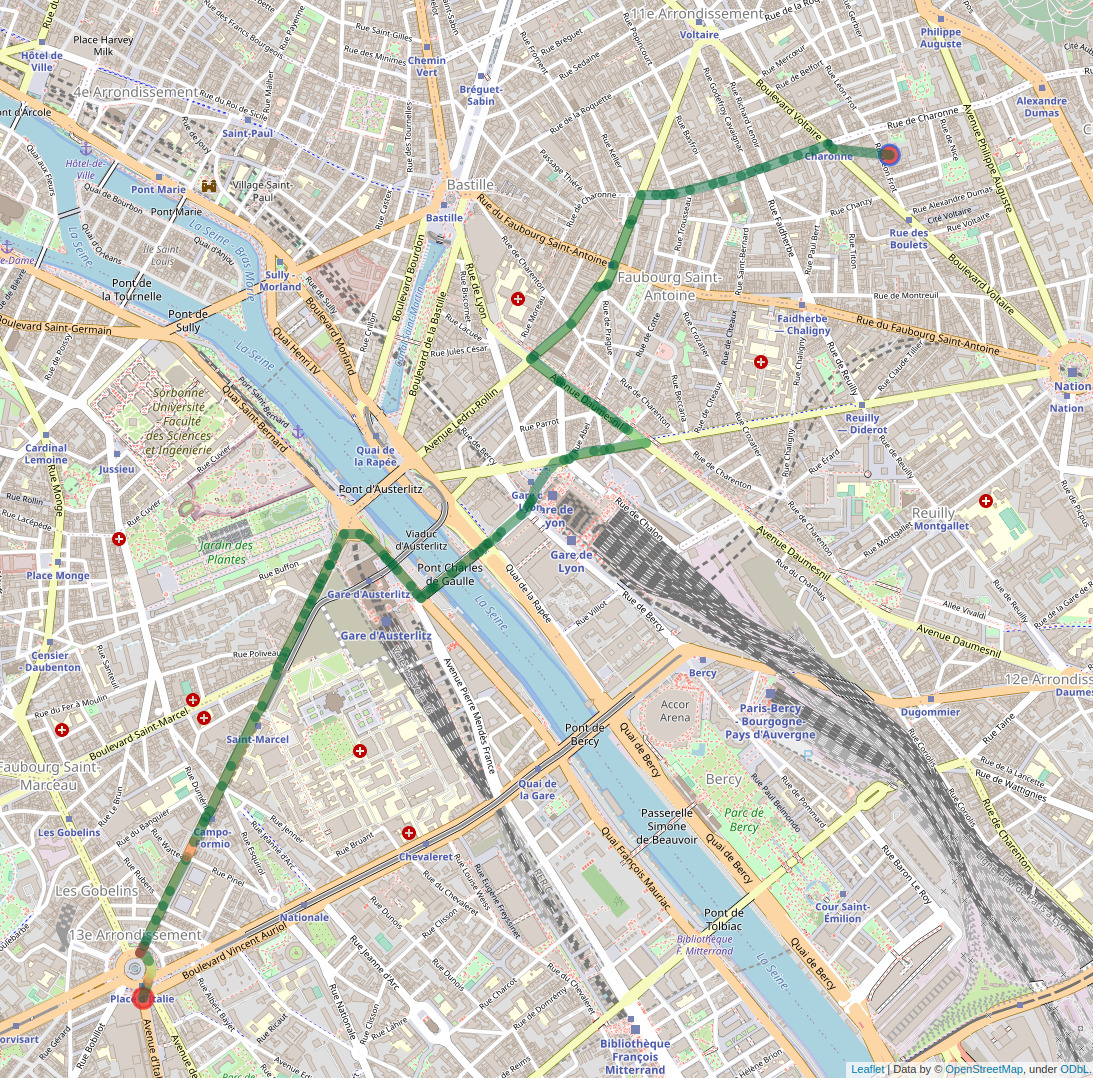
- Route choice: choose the route that minimizes the travel time of the agent for the departure time chosen
- Mode choice: choose the mode of the agent, given the expected utility for each mode available (Logit model, deterministic model or any other choice model)
- Output: mode, departure-time and route chosen by each agent
Note. For some modes, there is no departure-time and route choice.
Bottleneck Equation
\[ C = \alpha \cdot {tt} + \beta \cdot [t^* - t_a]_+ + \gamma \cdot [t_a - t^*]_+ \]Day-to-Day Model
- Input: expected and simulated time-dependent travel-time function for each road
- Compute the expected travel-time functions for next iteration given the expected and simulated travel-time functions of current iteration, using a Markov process (e.g., exponential process with weight $\lambda$ for simulated values)
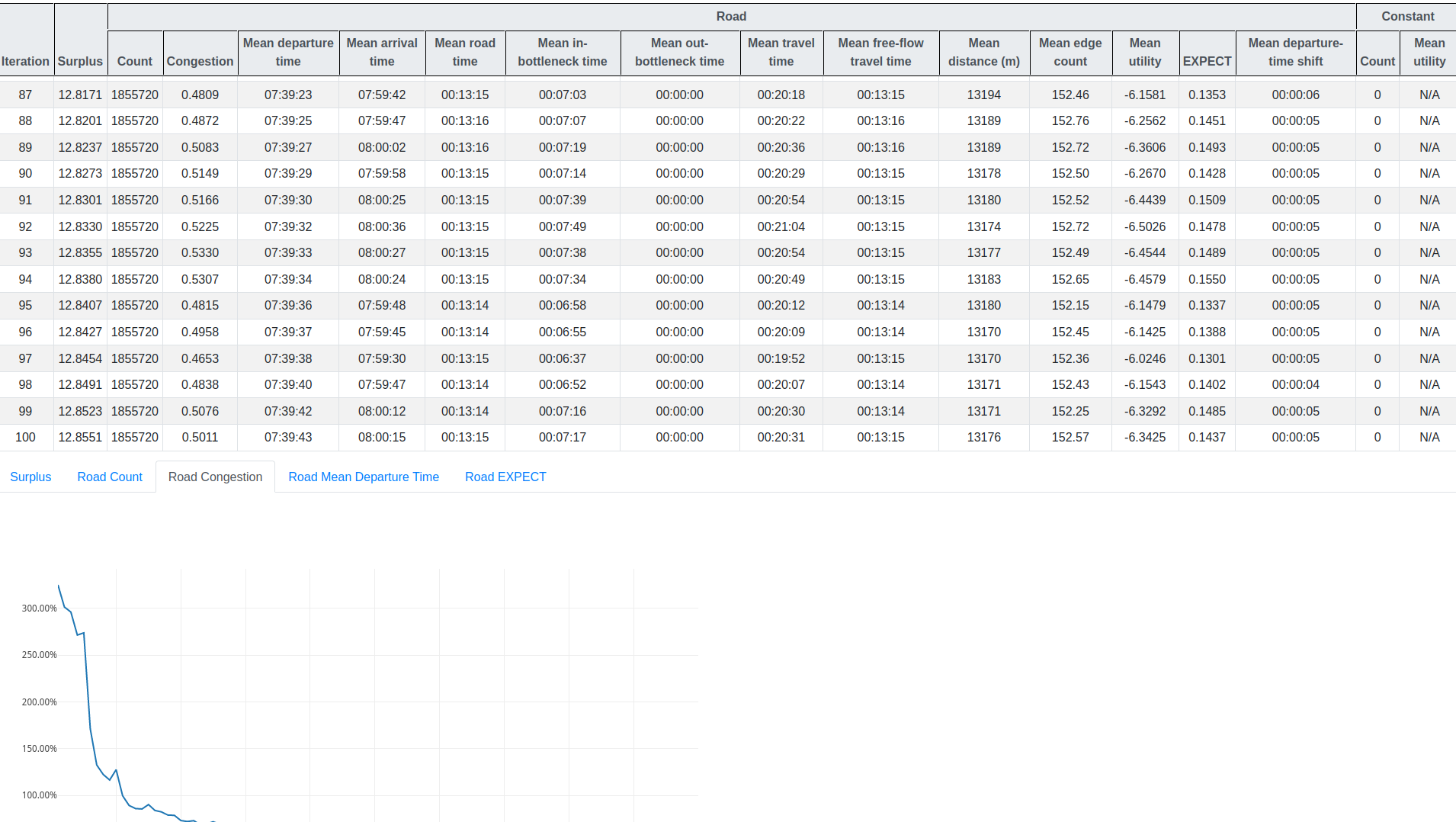
- Stop the simulation if a stopping criteria is reached (e.g., maximum number of iterations, EXPECT threshold, departure-time shift threshold)
- Output: expected time-dependent travel-time function for each road
Exponential Markov process: \[ Y_t = \lambda \cdot X_{t} + (1 - \lambda) \cdot Y_{t-1} \]
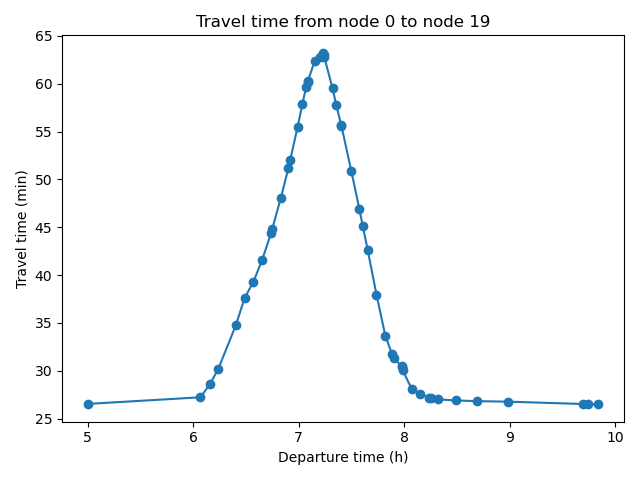
Results